วันอังคารที่ 23 เมษายน พ.ศ. 2556

รูปสามเหลี่ยม (Triangle) : เรขาคณิต

ชม 282,675 ครั้ง

รูปสามเหลี่ยม (Triangle) คือ หนึ่งในรูปร่างพื้นฐานในเรขาคณิต เป็นรูป 2 มิติ ที่ประกอบด้วยจุดยอด 3 จุดและด้าน 3 ด้านที่เป็นส่วนของเส้นตรง
ชนิดของรูปสามเหลี่ยม รูปสามเหลี่ยมแบ่งชนิดตามความยาวของด้านได้ดังนี้

รูปสามเหลี่ยมด้านเท่า มีด้านทุกด้านยาวเท่ากัน รูปสามเหลี่ยมด้านเท่าจะเป็นรูปมุมเท่าอีกด้วย นั่นคือ มุมภายในทุกมุมจะมีขนาดเท่ากัน คือ 60°
รูปสามเหลี่ยมหน้าจั่ว มีด้านสองด้านยาวเท่ากัน รูปสามเหลี่ยมหน้าจั่วจะมีมุมสองมุมมีขนาดเท่ากัน
รูปสามเหลี่ยมด้านไม่เท่า ด้านทุกด้านจะมีความยาวแตกต่างกัน มุมภายในในรูปสามเหลี่ยมด้านไม่เท่าจะมีขนาดเแตกต่างกัน


รูปสามเหลี่ยมด้านเท่า	รูปสามเหลี่ยมหน้าจั่ว	รูปสามเหลี่ยมด้านไม่เท่า

รูปสามเหลี่ยมแบ่งชนิดตามขนาดของมุมภายในที่ใหญ่ที่สุด อธิบายด้วยองศา

รูปสามเหลี่ยมมุมฉาก มีมุมภายในมุมหนึ่งมีขนาด 90° (มุมฉาก) ด้านที่อยู่ตรงข้ามกับมุมฉาก คือ ด้านตรงข้ามมุมฉาก ซึ่งเป็นด้านที่ยาวที่สุดในรูปสามเหลี่ยมมุมฉาก อีกสองด้าน คือ ด้านประกอบมุมฉาก
รูปสามเหลี่ยมมุมป้าน มีมุมภายในมุมหนึ่งมีขนาดใหญ่กว่า 90° (มุมป้าน)
รูปสามเหลี่ยมมุมแหลม มุมภายในทุกมุมมีขนาดเล็กกว่า 90° (มุมแหลม)


รูปสามเหลี่ยมมุมฉาก	รูปสามเหลี่ยมมุมป้าน	รูปสามเหลี่ยมมุมแหลม

ข้อเท็จจริงพื้นฐาน

ยุคลิดได้แสดงข้อเท็จจริงพื้นฐานเกี่ยวกับรูปสามเหลี่ยมไว้ในหนังสือ Elements เล่ม 1-4 เมื่อราวๆ 300 ปีก่อนคริสตกาล รูปสามเหลี่ยมเป็น รูปหลายเหลี่ยม และเป็น 2-ซิมเพล็กซ์ (2-simplex) รูปสามเหลี่ยม 2 รูป จะเรียกว่าคล้ายกัน ก็ต่อเมื่อ มุมของรูปสามเหลี่ยมหนึ่ง มีขนาดเท่ากับมุมที่สมนัยกันของอีกรูปสามเหลี่ยมหนึ่ง ด้านที่สมนัยกันจะเป็นสัดส่วนกัน ตัวอย่างเช่น รูปสามเหลี่ยม 2 รูปที่มีมุมร่วมกันมุมหนึ่ง และด้านที่ตรงข้ามกับมุมนั้นขนานกัน ฟังก์ชันตรีโกณมิติ ไซน์ และ โคไซน์ สามารถนิยามขึ้นจากรูปสามเหลี่ยมมุมฉากและเรื่องความคล้ายกันได้ ฟังชันก์เหล่านี้เป็นฟังก์ชันของมุม ซึ่งดูได้ในตรีโกณมิติ พิจารณา รูปสามเหลี่ยมที่ประกอบด้วยจุดยอด A, B และ C, มุม α, β และ γ และด้าน a, b และ c ด้าน a อยู่ตรงข้ามกับ จุดยอด A และมุม α และทำนองเดียวกับด้านอื่นๆ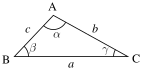

รูปสามเหลี่ยมที่ประกอบด้วย จุดยอด, ด้าน และมุมที่กำกับสัญลักษณ์

ในเรขาคณิตแบบยุคลิด ผลรวมของมุม α + β + γ จะเท่ากับสองมุมฉาก (180° หรือ π เรเดียน) ซึ่งทำให้เรารู้ขนาดของมุมที่สามได้ เมื่อรู้ขนาดของมุมเพียง 2 มุม

ทฤษฎีบทพีทาโกรัส

ทฤษฎีบทพีทาโกรัส (Pythagorean theorem) กล่าวว่าในรูปสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านตรงข้ามมุมฉาก จะเท่ากับ ผลรวมของพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านอีกสองด้านที่เหลือ ถ้าจุดยอด C เป็นมุมฉาก จะได้ว่า

$c^2 = a^2 + b^2,$

นั่นหมายความว่า ถ้ารู้ความยาวของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก ก็เพียงพอที่จะคำนวณด้านที่สาม ซึ่งเป็นลักษณะเฉพาะของรูปสามเหลี่ยมมุมฉาก ทฤษฎีบทพีทาโกรัสสามารถทำให้อยู่ในรูปทั่วไปโดยกฎโคไซน์ (law of cosines) ได้ว่า

$c^2 = a^2 + b^2 - 2ab cosgamma,$

ซึ่งใช้ได้กับทุกรูปสามเหลี่ยม แม้ว่า γ จะไม่เป็นมุมฉาก กฎโคไซน์ใช้คำนวณความยาวของด้านและขนาดของมุมของรูปสามเหลี่ยมได้ เมื่อรู้ความยาวของด้านทั้งสามด้าน หรือ รู้ความยาวของด้านทั้งสองที่อยู่ติดกับมุมที่รู้ขนาด
กฎไซน์ (law of sines) กล่าวว่า

$rac{sinalpha}a=$

เมื่อ d คือเส้นผ่านศูนย์กลางของวงกลมล้อม (วงกลมที่เล็กที่สุด ที่สามารถบรรจุรูปสามเหลี่ยมไว้ภายในได้พอดี) กฎไซน์ใช้คำนวณความยาวของด้านของรูปสามเหลี่ยมได้ เมื่อรู้ขนาดของมุม 2 มุมและด้าน 1 ด้าน ถ้ารู้ความยาวของด้าน 2 ด้านและขนาดของมุมที่ไม่อยู่ติดกัน กฎไซน์ก็สามารถใช้ได้เช่นเดียวกัน อย่างไรก็ตาม ในกรณีนี้อาจมีไม่มีคำตอบ หรืออาจมี 1 หรือ 2 คำตอบ

จุด, เส้น และวงกลมที่เกี่ยวข้องกับรูปสามเหลี่ยม

ศูนย์กลางวงล้อม คือจุดศูนย์กลางของวงกลมที่ลากผ่านจุดยอดทั้งสามของรูปสามเหลี่ยม

เส้นแบ่งครึ่งตั้งฉาก (perpendicular bisector) คือ เส้นตรงที่ลากผ่านจุดกึ่งกลางของด้าน และตั้งฉากกับด้านนั้น นั่นคือ ทำมุมฉากกับด้านนั้น เส้นแบ่งครึ่งตั้งฉากทั้งสามจะพบกันที่จุดเดียว คือ ศูนย์กลางวงล้อม (circumcenter) ของรูปสามเหลี่ยม จุดนี้เป็นจุดศูนย์กลางของวงกลมล้อม(circumcircle) ซึ่งเป็นวงกลมที่ลากผ่านจุดยอดทั้งสาม เส้นผ่านศูนย์กลางของวงกลมสามารถหาได้จากกฎไซน์ที่กล่าวไปในข้างต้น
ทฤษฎีบทของธาลีส (Thales' theorem) กล่าวว่า ถ้าศูนย์กลางวงล้อมอยู่บนด้านใดด้านหนึ่งของรูปสามเหลี่ยมแล้ว มุมตรงข้ามด้านนั้นจะเป็นมุมฉาก นอกจากนี้ ถ้าศูนย์กลางวงล้อมอยู่ในรูปสามเหลี่ยมแล้ว รูปสามเหลี่ยมนั้นเป็นรูปสามเหลี่ยมมุมแหลม ถ้าศูนย์กลางวงล้อมอยู่นอกรูปสามเหลี่ยมแล้ว รูปสามเหลี่ยมนั้นเป็นรูปสามเหลี่ยมมุมป้าน

จุดตัดของส่วนสูงคือ จุดออร์โทเซนเตอร์

ส่วนสูง (altitude) ของรูปสามเหลี่ยม คือ เส้นตรงที่ลากผ่านจุดยอดและตั้งฉาก(ทำมุมฉาก)กับด้านตรงข้าม ด้านตรงข้ามนั้นเรียกว่าฐาน (base) ของส่วนสูง และจุดที่ส่วนสูงตัดกับฐาน (หรือส่วนที่ขยายออกมา)นั้นเรียกว่า เท้า (foot) ของส่วนสูง ความยาวของส่วนสูงคือระยะทางระหว่างฐานกับจุดยอด ส่วนสูงทั้งสามจะตัดกันที่จุดเดียว เรียกจุดนั้นว่า จุดออร์โทเซนเตอร์(orthocenter) ของรูปสามเหลี่ยม จุดออร์โทเซนเตอร์จะอยู่ในรูปสามเหลี่ยมก็ต่อเมื่อรูปสามเหลี่ยมนั้นไม่เป็นรูปสามเหลี่ยมมุมป้าน จุดยอดทั้งสามและจุดออร์โทเซนเตอร์นั้นอยู่ในระบบออร์โทเซนตริก (orthocentric system)

จุดตัดของเส้นแบ่งครึ่งมุม ใช้หาจุดศูนย์กลางของวงกลมแนบใน

เส้นแบ่งครึ่งมุม (angle bisector) คือ เส้นตรงที่ลากผ่านจุดยอด ซึ่งแบ่งมุมออกเป็นครึ่งหนึ่ง เส้นแบ่งครึ่งมุมทั้งสามจะตัดกันที่จุดเดียว คือ จุดศูนย์กลางของวงกลมแนบใน (incircle) ของรูปสามเหลี่ยม วงกลมแนบในคือวงกลมที่อยู่ในรูปสามเหลี่ยม และสัมผัสด้านทั้งสาม มีอีกสามวงกลมที่สำคัญคือ วงกลมแนบนอก (excircle) คือวงกลมที่อยู่นอกรูปสามเหลี่ยมและสัมผัสกับด้านหนึ่งด้านและส่วนที่ขยายออกมาทั้งสอง จุดศูนย์กลางของวงกลมแนบในและวงกลมแนบนอกอยู่ในระบบออร์โทเซนตริก

เซนทรอยด์ เป็นศูนย์ถ่วง

เส้นมัธยฐาน (median) ของรูปสามเหลี่ยม คือ เส้นตรงที่ลากผ่านจุดยอดและจุดกึ่งกลางของด้านตรงข้าม ซึ่งจะแบ่งรูปสามเหลี่ยมออกเป็นพื้นที่ที่เท่ากัน เส้นมัธยฐานทั้งสามจะตัดกันที่จุดเดียว คือ เซนทรอยด์ (centroid) ของรูปสามเหลี่ยม จุดนี้จะเป็นศูนย์ถ่วง (center of gravity) ของรูปสามเหลี่ยมด้วย ถ้ามีไม้ที่เป็นรูปสามเหลี่ยม คุณสามารถทำให้มันสมดุลได้ที่เซนทรอยด์ของมันหรือเส้นใดๆที่ลากผ่านเซนทรอยด์ เซนทรอยด์จะแบ่งเส้นมัธยฐานด้วยอัตราส่วน 2:1 นั่นคือระยะทางระหว่างจุดยอดกับเซนทรอยด์ จะเป็นสองเท่าของระยะทางระหว่างเซนทรอยด์กับจุดกึ่งกลางของด้านตรงข้าม

วงกลมเก้าจุด แสดงความสมมาตรที่จุดหกจุดอยู่บนวงกลมเดียวกัน

จุดกึ่งกลางของด้านทั้งสาม และเท้าของส่วนสูงทั้งสาม จะอยู่บนวงกลมเดียวกัน คือ วงกลมเก้าจุด (nine point circle) ของรูปสามเหลี่ยม อีกสามจุดที่เหลือคือจุดกึ่งกลางระหว่างจุดยอดกับจุดออร์โทเซนเตอร์ ซึ่งเป็นส่วนหนึ่งของส่วนสูง รัศมีของวงกลมเก้าจุดจะเป็นครึ่งหนึ่งของรัศมีวงกลมล้อม มันจะสัมผัสวงกลมแนบใน (ที่จุด Feuerbach) และสัมผัสวงกลมแนบนอก

เส้นออยเลอร์ คือเส้นที่ลากผ่าน เซนทรอยด์ (สีเหลือง), จุดออร์โทเซนเตอร์ (สีน้ำเงิน),
ศูนย์กลางวงล้อม (สีเขียว) และจุดศูนย์กลางของวงกลมเก้าจุด (สีแดง)

          เซนทรอยด์ (สีเหลือง), จุดออร์โทเซนเตอร์ (สีน้ำเงิน), ศูนย์กลางวงล้อม (สีเขียว) และจุดศูนย์กลางของวงกลมเก้าจุด (จุดสีแดง) ทั้งหมดจะอยู่บนเส้นเดียวกัน ที่เรียกว่า เส้นออยเลอร์ (Euler's line) (เส้นสีแดง) จุดศูนย์กลางของวงกลมเก้าจุดจะอยู่กึ่งกลางระหว่างจุดออร์โทเซนเตอร์กับศูนย์กลางวงล้อม ระยะทางระหว่างเซนทรอยด์กับศูนย์กลางวงล้อมจะเป็นครึ่งหนึ่งของระยะทางระหว่างเซนทรอยด์กับจุดออร์โทเซนเตอร์
          จุดศูนย์กลางของวงกลมแนบในโดยทั่วไปจะไม่อยู่บนเส้นออยเลอร์
          ภาพสะท้อนของเส้นมัธยฐานที่เส้นแบ่งครึ่งมุมของจุดยอดเดียวกัน เรียกว่า symmedian symmedianทั้งสามจะตัดกันที่จุดเดียว คือ จุด symmedian (symmedian point) ของรูปสามเหลี่ยม

การหาพื้นที่ของรูปสามเหลี่ยม

การคำนวณพื้นที่ของรูปสามเหลี่ยมเป็นปัญหาพื้นฐานที่พบเจอเป็นประจำในสถานการณ์ต่างๆ มีหลายวิธีที่จะหาคำตอบ ขึ้นอยู่กับว่าเรารู้อะไรเกี่ยวกับรูปสามเหลี่ยมบ้าง วิธีเหล่านี้เป็นสูตรหาพื้นที่ของรูปสามเหลี่ยมที่ใช้กันบ่อยๆ

ใช้เรขาคณิต

พื้นที่ S ของรูปสามเหลี่ยม คือ S = ½bh เมื่อ b คือความยาวของด้านใดๆในรูปสามเหลี่ยม (ฐาน) และ h (ส่วนสูง) คือระยะทางตั้งฉากระหว่างฐานกับจุดยอดที่ไม่ใช่ฐาน วิธีนี้แสดงให้เห็นได้ด้วยการสร้างรูปทางเรขาคณิต

เปลี่ยนรูปสามเหลี่ยมเป็นรูปสี่เหลี่ยมด้านขนาน ที่มีพื้นที่เป็นสองเท่าของรูปสามเหลี่ยม จากนั้นเปลี่ยนเป็นรูปสี่เหลี่ยมมุมฉาก

เพื่อที่จะหาพื้นที่ของรูปสามเหลี่ยมที่กำหนดให้ (สีเขียว) ขั้นแรก นำรูปสามเหลี่ยมเดียวกัน หมุนไป 180° และวางมันบนด้านหนึ่งของรูปสามเหลี่ยมที่กำหนดให้ เพื่อให้เป็นรูปสี่เหลี่ยมด้านขนาน จากนั้นตัดส่วนหนึ่งของรูปและนำไปวางบนอีกด้านหนึ่ง เพื่อให้เป็นรูปสี่เหลี่ยมมุมฉาก เนื่องจากพื้นที่ของรูปสี่เหลี่ยมมุมฉากเท่ากับ bh ฉะนั้น พื้นที่ของรูปสามเหลี่ยมที่กำหนดให้จึงเท่ากับ ½bh

พื้นที่ของรูปสี่เหลี่ยมด้านขนาน เท่ากับ ผลคูณไขว้ของสองเวกเตอร์

ใช้เวกเตอร์

พื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถคำนวณได้ด้วยเวกเตอร์ ถ้า AB และ AC เป็นเวกเตอร์ที่ชี้จาก A ไป B และ A ไป C ตามลำดับ พื้นที่ของรูปสี่เหลี่ยมด้านขนาน ABCD คือ |AB × AC| หรือขนาดของผลคูณไขว้ของเวกเตอร์ AB กับ AC |AB × AC| มีค่าเท่ากับ |h × AC| เมื่อ h แทนเวกเตอร์ส่วนสูง
พื้นที่ของรูปสามเหลี่ยม ABC เป็นครึ่งหนึ่งของพื้นที่ของรูปสี่เหลี่ยมด้านขนาน หรือ S = ½|AB × AC|

ใช้ตรีโกณมิติหาส่วนสูง h

ใช้ตรีโกณมิติ

ส่วนสูงของรูปสามเหลี่ยมหาได้ด้วยตรีโกณมิติ จากรูปทางซ้าย ส่วนสูงจะเท่ากับ h = a sin γ นำไปแทนในสูตร S = ½bh ที่ได้จากข้างต้น จะได้พื้นที่ของรูปสามเหลี่ยมเท่ากับ S = ½ab sin γ
พื้นที่ของรูปสี่เหลี่ยมด้านขนาน จึงเท่ากับ ab sin γ

ใช้พิกัด

ถ้าจุดยอด A อยู่ที่จุดกำเนิด (0, 0) ในระบบพิกัดคาร์ทีเซียน และกำหนดให้พิกัดของอีกสองจุดยอดอยู่ที่ B = (x₁, y₁) และ C = (x₂, y₂) แล้วพื้นที่ S จะคำนวณได้จาก 1/2 เท่าของค่าสัมบูรณ์ของดีเทอร์มิแนนต์

$egin{vmatrix}x_1 & x_2 y_1 & y_2 end{vmatrix}$

หรือ S = ½ |x₁y₂ − x₂y₁|

ใช้สูตรของเฮรอน

อีกวิธีที่ใช้คำนวณ S ได้คือใช้สูตรเฮรอน

$S = sqrt{s(s-a)(s-b)(s-c)}$

เมื่อ s = ½ (a + b + c) คือครึ่งหนึ่งของเส้นรอบรูปของรูปสามเหลี่ยม

ใช้ความยาวด้านและสูตรที่เสถียรเชิงตัวเลข

สูตรเฮรอนนั้นไม่เสถียรเชิงตัวเลขสำหรับรูปสามเหลี่ยมที่มีมุมขนาดเล็กมากๆ วิธีที่ดีกว่าคือ เรียงความยาวของด้านตามนี้ a ≥ b ≥ c และคำนวณจาก

$S = 1/4sqrt{(a+(b+c)) (c-(a-b)) (c+(a-b)) (a+(b-c))}$

วงเล็บในสูตรนั้น จำเป็นต้องใส่ตามลำดับเพื่อป้องกันความไม่เสถียรเชิงตัวเลขในการหาค่า

รูปสามเหลี่ยมที่ไม่อยู่บนระนาบ

ถ้ามีส่วนประกอบของรูปสามเหลี่ยม (จุดยอด หรือด้าน) 4 ส่วน อยู่บนระนาบเดียวกันแล้ว รูปสามเหลี่ยมนั้นจะอยู่บนระนาบเดียวกัน นักเรขาคณิตได้ศึกษารูปสามเหลี่ยมที่ไม่อยู่บนระนาบด้วย ตัวอย่างเช่น รูปสามเหลี่ยมบนทรงกลมในเรขาคณิตทรงกลม และ รูปสามเหลี่ยมเชิงไฮเพอร์โบลาในเรขาคณิตเชิงไฮเพอร์โบลา

สัญลักษณ์ทางคณิตศาสตร์

: Maths symbols

รายการต่อไปนี้เป็นการแสดงสัญลักษณ์โดยทั่วไปที่ใช้ในคณิตศาสตร์ จะต้องใช้และตระหนักในการใช้ (อักษร n และ m ถูกใช้เพื่อความเหมาะสมในการแสดงค่าใดๆ ที่กำหนดให้)

+ เครื่องหมายบวก

เช่น 2 + 5 = 7

- เครื่องหมายลบ

เช่น 23 - 5 = 18

× เครื่องหมายคูณ

เช่น 6 × 5 = 30

÷ เครื่องหมายหาร

เช่น 45 ÷ 9 = 5

n² จำนวนยกกำลังสอง

เช่น 4² = 4 x 4

n³ จำนวนยกกำลังสาม

เช่น 3³ = 3 x 3 x 3

√n รากที่สอง

เช่น √49=7

∛n รากที่สาม

เช่น ∛8=2

% เปอร์เซนต์

เช่น 0.5 = 50%

n จำนวนบวก

เช่น 2 x 3 = 6

-n จำนวนลบ

เช่น 3 x (-4) = -12

± จำนวนบวกหรือจำนวนลบ

เช่น ±5 คือ 5 หรือ -5

n : m อัตราส่วน

เช่น 5 : 2

∝ เป็นสัดส่วนกับ

n° องศา

เช่น ขนาดของมุมรูปจุดศูนย์กลางของวงกลม เท่ากับ 360°

ค่าพาย

มีค่าประมาณ 3.141592654...

∠ มุม

เช่น มุมฉากมีขนาด 90º

∟ มุมฉาก

θ มุมที่ไม่ทราบค่า ทีตา

α มุมที่ไม่ทราบว่า แอลฟา

≡ เครื่องหมายเอกลักษณ์

เช่น 3x ≡ 5x - 2x

< น้อยกว่า

เช่น 1 < 3

> มากกว่า

เช่น 3 > 1

≤ น้อยกว่าหรือเท่ากับ

≥ มากกว่าหรือเท่ากับ

≠ ไม่เท่ากับ

≈ ค่าประมาณ

เช่น 100 ÷ 9 ≈ 10

∑ ผลรวม

{n} เซต

เช่น A = {2,5,8,9}

∈ เป็นสมาชิกของ

เช่น 3 ∈ {1,2,3,4}

∉ ไม่เป็นสมาชิกของ

เช่น 4 ∉ {5,6,8}

U เอกภพสัมพัทธ์

{ } หรือ Φ เซตว่าง

υ ยูเนียน หรือถ้วย

เช่น {3,5,8} υ {1,2,3} = {1,2,3,5,8}

∩ อิเตอร์เซกชัน หรือหมวก

เช่น {3,5,8} ∩ {1,2,3} = {3}

อาชีพ "นักคณิตศาสตร์ประกันภัย"

จากข่าวที่ปรากฏบนหน้าหนังสือพิมพ์ The Philadelphia Inquirer ฉบับวันที่ 20 พฤษภาคม 2531 ซึ่งได้มาจากหนังสือที่ตีพิมพ์เป็นเล่ม ชื่อ "The Job Almanac" พิมพ์โดย American Reference Inc. แห่งเมืองชิคาโก สหรัฐอเมริกา ดังปรากฏข้อความในหน้าแรกของบทความนี้ เป็นผลของการสำรวจอาชีพยอดนิยม ซึ่งเป็นที่ชื่นชมของคนอเมริกัน จากทั้งหมด 250 อาชีพ โดยพิจารณาจากเกณฑ์ 6 อย่าง ประกอบด้วย เงินเดือน ความกดดัน สภาพแวดล้อมของการทำงาน โอกาสในอนาคต หลักประกันความมั่นคง และความเหนื่อยยากของร่างกาย ผลปรากฎว่า อาชีพ "Actuary" ได้รับการยกย่องว่าเป็นอาชีพที่ดีที่สุดเป็นอันดับหนึ่ง อันดับรองลงมาได้แก่ อาชีพโปรแกรมเมอร์ นักวิเคราะห์ระบบคอมพิวเตอร์ นักคณิตศาสตร์ และนักสถิติ ตามลำดับ อนึ่ง อาชีพที่ดีที่สุดเป็นอันดับหนึ่งในที่นี้เป็นการจัดอันดับเมื่อพิจารณาจากเกณฑ์ 6 อย่างข้างต้นประกอบเข้าด้วยกัน แต่อาชีพดังกล่าว อาจไม่เป็นอันดับหนึ่งถ้าพิจารณาในแต่ละเกณฑ์ นั้นคือ อาจไม่ใช่อาชีพที่ได้เงินเดือนมากที่สุด หรือมีชื่อเสียงมากที่สุด ก็เป็นได้

ผลจากการสำรวจดังกล่าวข้างต้น คงทำให้หลาย ๆ ท่านเกิดความสังสัย พร้อมกับอาจเกิดคำถามในใจว่า "อาชีพอะไรกัน... Actuary..? ทำไมถึงได้รับยกย่องจากคนอเมริกันว่าเป็นอาชีพที่ดีสุดได้"

ถ้าบอกว่า อาชีพ "Actuary" ที่เป็นข่าวในหน้าแรกของบทความนี้ว่าเป็นอาชีพที่ดีที่สุดของคนอเมริกัน คือ "อาชีพนักคณิตศาสตร์ประกันภัย" นั่นเอง ท่านรู้จักไหม

นักคณิตศาสตร์ประกันภัย คือ ใคร

หากท่านไม่เคยได้ยินชื่อ นักคณิตศาสตร์ประกันภัยมาก่อนเลย ก็ไม่ใช่เรื่องแปลกประหลาด แม้แต่ในอเมริกา ซึ่งถือว่าเป็นประเทศที่มีความเจริญทางด้านประกันภัยเป็นอย่างมาก โดยเฉพาะการประกันชีวิตจัดว่ามีบทบาทต่อชีวิตประจำวันของคนอเมริกัน ก็ยังมีคนอเมริกันจำนวนไม่น้อยที่ไม่รู้จักนักคณิตศาสตร์ประกันภัย ซึ่งอาจเป็นเพราะนักคณิตศาสตร์ประกันภัยส่วนใหญ่ชอบทำงานอยู่เบี้องหลังความสำเร็จของบริษัทประกันภัย

สำหรับศาสตร์ที่เกี่ยวข้องกับสาขาวิชาทางด้านคณิตศาสตร์ประกันภัย ก็คือ คณิตศาสตร์ประกันภัย หรือที่เรียกกันว่า "Actuarial Science"

นักคณิตศาสตร์ประกันภัย คือ บุคคลซึ่งใช้เทคนิคทางคณิตศาสตร์และสถิติในการวิเคราะห์และประมาณการเกิดเหตุการณ์ ซึ่งอาจเกิดขึ้นได้กับคนทุกคนในอนาคต เช่น การเกิด การเจ็บป่วย การเกิดอุบัติเหตุ การพิการ การเกษียณอายุ การว่างงาน เป็นต้น เพื่อช่วยให้ประมาณเหตุการณ์ซึ่งน่าจะเกิดขึ้นได้ในอนาคตได้ใกล้เคียงความเป็นจริง โดยการจัดทำในรูปของตาราง เช่น ตารางมรณะ และตารางสุขภาพ (Mortality and Morbidity Experience Tables) แล้วนำผลที่ได้มาใช้ประกอบกับความรู้ด้านการบริหารและการเงิน เพื่อคำนวณอัตราเบี้ยประกันเงินสำรอง และตัวเลขข้อเท็จจริงอื่น ๆ ทางการเงิน ซึ่งจะทำให้บริษัทประกันภัยสามารถดำเนินกิจการได้อย่างราบรื่น มั่นคง และสามารถให้ความคุ้มครองแก่ผู้เอาประกัน หรือผู้รับประโยชน์ได้

นอกจากนี้ นักคณิตศาสตร์ประกันภัยยังต้องมีความเข้าใจ ในการดำเนินงานทั้งหมดของธุรกิจประกันภัยจะถือเป็นข้อผูกมัดทางการเงินของบริษัทในระยะยาว เป็นเวลาหลาย ๆ ปี จึงมีอิทธิพลอย่างมากต่อนโยบายและการดำเนินงานอย่างเป็นระบบของบริษัท ด้วยเหตุนี้ นักคณิตศาสตร์ประกันภัยจึงต้องเกี่ยวข้องกับการดำเนินธุรกิจในหลายขั้นตอน เช่น การจัดการทั่วไป การตลาด การวิจัย การพิจารณารับประกัน การลงทุน การบัญชี การบริหาร และการวางแผนระยะยาว

จากความหมายดังกล่าวข้างต้น อาจกล่าวอีกอย่างหนึ่งได้ว่า นักคณิตศาตร์ประกันภัยคือ นักธุรกิจมืออาชีพซึ่งใช้ความเชี่ยวชาญทางคณิตศาสตร์เพื่อกำหนด วิเคราะห์ แก้ปัญหาทางสังคม และทางการเงิน โดยการสร้างโปรแกรมที่จะลดความเสี่ยงทางการเงินของการเกิดเหตุการณ์ที่อาจคาดการณ์ได้ หรือคาดการณ์ไม่ได้ ซึ่งเกิดขึ้นได้กับมนุษย์ นั่นเอง

หน้าที่ความรับผิดชอบของนักคณิตศาสตร์ประกับภัย

จากบทบาทของนักคณิตศาสตร์ประกันภัยดังที่ได้กล่าวมาแล้ว อาจกล่าวได้ว่า หน้าที่และความรับผิดชอบของนักคณิตศาสตร์ประกันภัยอาจรวมถึง

1. นักคณิตศาสตร์ประกันภัยต้องแน่ใจว่า บริษัทประกันภัยมีเงินสดสำรองในมือเพียงพอที่จะจ่ายเงินผลประโยชน์ หรือเงินสินไหมทดแทน ตลอดจนค่าใช้จ่ายต่าง ๆ เมื่อมีการเรียกร้องค่าสินไหมทดแทน หรือเงินเลี้ยงชีพ จากผู้เอาประกัน หรือผู้รับประโยชน์

2. พิจารณากำหนดอัตราเบี้ยประกันที่บริษัทเรียกเก็บจากผู้เอาประกัน ให้มีความยุติธรรมเพียงพอ และสามารถทำให้บริษัทดำเนินกิจการต่อไปได้อย่างราบรื่น และมั่นคง

3. ปรับปรุง และพัฒนาผลิตกรมธรรม์แบบใหม่ ๆ เพื่อสนองความต้องการของสังคมอยู่เสมอ

4. ให้คำแนะนำเจ้าหน้าที่ของบริษัท ในการพิจารณารับประกันว่า รายใดที่รับได้และรายใดที่ควรปฎิเสธ เพราะเหตุใด หากจะรับได้แต่ต้องเพิ่มเบี้ยประกันควรจะเพิ่มในอัตราเท่าใด

5. มีส่วนร่วมในการแสดงความคิดเห็นเกี่ยวกับการดำเนินงานของบริษัทในด้านต่าง ๆ

6. เตรียมจัดทำรายงานประจำปี แสดงสถานะทางการเงินของบริษัท เพื่อเสนอต่อสำนักงานประกันภัย และผู้ถือหุ้นของบริษัท

7. วิเคราะห์ผลการดำเนินงานที่ผ่านมาทั้งหมดของบริษัทเมื่อสิ้นปีปฏิทิน เช่น การใช้ข้อสมมุติเกี่ยวกับอัตรามรณะ ค่าใช้จ่าย อัตราดอกเบี้ยจากการลงทุน วิเดราะห์การขาดอายุของกรมธรรม์ เงินคงเหลือจากการดำเนินธุรกิจ เป็นต้น แล้วนำผลที่ได้มาประเมิน และสรุปว่าธุรกิจควรดำเนินต่อไปในทิศทางใด ส่วนใดควรปรับปรุงแก้ไข แบบประกันใดควรยุบหรือยกเลิก หรือควรสนับสนุนต่อไป

การเตรียมตัวเพื่อเข้าสู่อาชีพนักคณิตศาสตร์ประกันภัย

"ถ้าท่านชอบคณิตศาสตร์ และอยากมีส่วนร่วมต่อสังคมอย่างมีคุณค่า อาชีพพนักคณิตศาสตร์ประกันภัยอาจเหมาะกับท่าน"

อาชีพนักคณิตศาสตร์ประกันภัยต้องการผู้มีความรู้ความสามารถทางคณิตศาสตร์เป็นอย่างดี เนื่องจาก งานที่ทำต้องเกี่ยวข้องกับการประยุกต์ใช้คณิตศาสตร์ประกอบกับความรู้ ความเชียวชาญทางธุรกิจ ดังนั้น ท่านต้องเป็นผู้มีความกระตือรือร้น มีเหตุมีผล มีความคิดริเริ่มสร้างสรรค์ และมีความสามารถในการตัดสินใจ

สำหรับนักเรียนชั้นมัธยมศึกษาตอนปลายที่คิดอยากเป็นนักคณิตศาสตร์ประกันภัย ท่านต้องเป็นผู้มีใจรักคณิตศาสตร์ และสอบได้คะแนนวิชาคณิตศาสตร์อยู่ในเกณฑ์สูงกว่าคะแนนเฉลี่ย

สำหรับนักศึกษามหาวิทยาลัยที่ต้องการเตรียมตัวเพื่อเข้าสู่อาชีพนักคณิตศาสตร์ประกันภัยในอนาคต ควรเลือกเรียนวิชาคณิตศาสตร์ไว้หลาย ๆ วิชาตลอดช่วง 4 ปี โดยเฉพาะวิชาพีชคณิตและการประยุกต์ ควรมีเวลาฝึกฝนให้มาก นอกจากนี้ควรเลือกเรียนวิชาทางแคลคูลัส ความน่าจะเป็น และสถิติศาสตร์

ท่านพึงระลึกถึงเสมอว่า ท่านกำลังเตรียมตัวเพื่อประกอบอาชีพในทางธุรกิจ ดังนั้น เพื่อความสำเร็จในอนาคต ท่านต้องมีการพัฒนาความคิด ความเข้าใจเกี่ยวกับสภาพแวดล้อมทางธุรกิจอย่างกว้างไกล วิชาการต่าง ๆ ทางธุรกิจที่สำคัญที่ท่านควรเลือกเรียนในมหาวิทยาลัย ได้แก่ การจัดการ บัญชี การเงิน ประกันภัย เศรษฐศาสตร์ และวิชาการทางคอมพิวเตอร์ ซึ่งนับเป็นวิชาที่มีบทบาทสำคัญ และนับเป็นเครื่องมือสำคัญของนักคณิตศาสตร์ประกันภัยในปัจจุบัน การผสมผสานความรู้ความเข้าใจในวิชาการต่าง ๆ ดังกล่าวจะทำให้ท่านพัฒนาความคิดได้อย่างมีประสิทธิภาพ และประสบความสำเร็จในอาชีพนี้

อาจกล่าวได้ว่า การเตรียมตัวที่ดีที่สุดเพื่อเข้าสู่อาชีพนักคณิตศาสตร์ประกันภัยคือ ท่านควรเลือกเรียนวิชาเอกทางด้านคณิตศาสตร์หรือสถิติ หรือวิชาเอกทางด้านบริหารธุรกิจ โดยมีวิชาโททางคณิตศาสตร์หรือสถิติ หรือวิชาเอกทางเศรษฐศาสตร์ โดยมีวิชาคณิตศาสตร์หรือสถิติเป็นวิชาโท

ในประเทศไทยขณะนี้ยังไม่มีมหาวิทยาลัยใดที่เปิดสอนวิชาเอกด้านคณิตศาสตร์ประกันภัยโดยตรง ส่วนใหญ่เปิดสอนเป็นวิชาด้านประกันภัย โดยเน้นหลักการทั่วไปของการประกันภัย ทั้งในส่วนของการประกันวินาศภัย และการประกันชีวิตมากกว่าสอนการคำนวณทางคณิตศาสตร์ประกันภัย โดยมีภาควิชาสถิติ คณะพาณิชยศาสตร์และการบัญชี จุฬาลงกรณ์มหาวิทยาลัยเป็นแห่งแรกที่เปิดสอนวิชาเอกด้านประกันภัย โดยมีวิธีด้านคณิตศาสตร์ประกันภัยเป็นวิชาในกลุ่มวิชาเอกนี้ นอกจากนี้ ในหลักสูตรปริญญาโทสถิติได้เปิดสอนวิชาด้านคณิตศาสตร์ประกันภัยในคณะวิทยาศาสตร์และเทคโนโลยี สาขาวิชาคณิตศาสตร์และสถิติ ซึ่งในอดีตที่ผ่านมาจนถึงปัจจุบันเปิดเป็นเพียงวิชาเลือกเท่านั้น ทั้งในหลักสูตรระดับปริญญาตรีและปริญญาโท แต่มีโครงการจะเปิดเป็นหลักสูตรวิชาโทคณิตศาสตร์ประกันภัยในปีการศึกษา 2533 ส่วนวิชาด้านประกันภัยทั่ว ๆ ไป ได้เปิดสอนอยู่แล้วในคณะพาณิชยศาสตร์และการบัญชี

ในประเทศสหรัฐอเมริกาและแคนาดามีมหาวิทยาลัยประมาณ 40 แห่งที่เปิดสอนหลักสูตรคณิตศาสตร์ประกันภัยที่สมบูรณ์แบบ ในระดับปริญญาตรีหรือปริญญาโท ซึ่งนับว่ามีจำนวนน้อย บางมหาวิทยาลัยจัดวิชาด้านนี้อยู่ในสาขาวิชาคณิตศาสตร์หรือสาขาวิชาสถิติ บางแห่งอาจจัดอยู่ในหลักสูตรบริหารธุรกิจ และบางแห่งจัดเป็นหลักสูตรร่วมกับคณะเศรษฐศาสตร์

อาชีพนักคณิตศาสตร์ประกันภัยในอเมริกา และ แคนาดา

การเป็นนักคณิตศาสตร์ประกันภัยที่มีมาตรฐานของอาชีพเป็นที่ยอมรับกันในอเมริกาและแคนาดา ถ้าท่านสนใจงานในด้านการประกันชีวิต (Life insurance) การประกันสุขภาพ (Health insurance) และการวางแผนเกี่ยวกับเงินเลี้ยงชีพ(Pension Planning) ท่านต้องผ่านการสอบของ Society of Actuaries (SOA) แต่ถ้าท่านสนใจงานทางด้านการประกันวินาศภัย (Casualty insurance) ท่านต้องผ่านการสอบของ Casualty Actuarial Society (CAS) ในที่นี้จะกล่าวถึงเฉพาะที่เกี่ยวข้องกับ SOA

ข้อสอบของสมาคม SOA มีทั้งหมด 10 ตอน ถ้าท่านผ่านการสอบทั้ง 10 ตอนท่านจะได้รับวุฒิบัตรเป็น Fellow ของสมาคม (F.S.A.) ซึ่งจัดเป็นคุณวุฒิสูงสุดสายอาชีพที่มีมาตรฐานเป็นที่ยอมรับทั่วโลก ความยากของการเป็น F.S.A. เปรียบเหมือนกับความยากในการทำปริญญาเอกทางคณิตศาสตร์ บริหารธุรกิจ หรือเศรษฐศาสตร์ ถ้าท่านสอบผ่านเพียง 5 ตอนแรก ท่านจะได้รับวุฒิบัตรเป็น Associate ของสมาคม (A.S.A.) และจะได้เป็นสมาชิกของสมาคม SOA ด้วย

การได้เป็น A.S.A. หรือ F.S.A. ของ SOA จะทำให้ท่านเป็นที่ยอมรับในมาตรฐานของวิชาชีพ และสามารถทำงานในบริษัทประกันชีวิตและหน่วยงานที่เกี่ยวข้องได้ทั่วโลก และได้รับค่าตอบแทนค่อนข้างสูง

จากข้อมูลในปี พ.ศ. 2527 พบว่า มีบริษัทประกันชีวิตและสุขภาพในอเมริกาและแคนาดาจำนวน 2,362 บริษัท และมีการว่าจ้างงานในหน่วยงานดังกล่าวถึงประมาณ 1 ล้านคน นอกจากนี้พบว่า มีประชาชนชาวอเมริกันสนใจทำประกันชีวิตถึงประมาณ200% กล่าวคือ โดยเฉลี่ยประชาชนแต่ละคนจะถือกรมธรรม์ประกันชีวิตคนละ 2 ฉบับ

จะเห็นได้ว่า อาชีพนักคณิตศาสตร์ประกันภัยนี้ ท่านไม่จำเป็นต้องจบด้านคณิตศาสตร์ประกันภัยโดยตรง เพียงแต่ท่านต้องสอบผ่านข้อสอบของ SOA หรือ CAS ท่านก็สามารถทำงานเป็นนักคณิตศาสตร์ประกันภัยได้ การเรียนจบด้านคณิตศาสตร์ประกันภัยจะช่วยให้ท่านผ่านการสอบ 5 ตอนแรกได้เร็วขึ้นเท่านั้น ด้วยเหตุนี้อาชีพนักคณิตศาสตร์ประกันภัยจึงเปิดกว้างสำหรับทุกท่านที่สนใจและมีคุณสมบัติเหมาะสม ดังที่ได้กล่าวมาแล้ว เท่าที่ผ่านมาพบว่า นักศึกษาที่สนใจเข้าสู่อาชีพนี้มักจะหาประสบการณ์โดยการฝึกงานภาคฤดูร้อนกับบริษัทประกันชีวิตและหน่วยงานที่เกี่ยวข้อง ซึ่งให้ความร่วมมือและสนับสนุนการฝึกงานของนักศึกษาเป็นอย่างมาก

อาชีพนักคณิตศาสตร์ประกันภัยในประเทศไทย

ในประเทศไทย ได้มีการก่อตั้งสมาคมคณิตศาสตร์ประกันภัยแห่งประเทศไทย (Acturial Association of Thailand) ขึ้นเป็นครั้งแรกในปี พ.ศ. 2517 โดยมีวัตถุประสงค์ที่จะส่งเสริมวิชาชีพคณิตศาสตร์ประกันภัยให้ก้าวหน้า เพื่อสามารถรับใช้ประเทศชาติในด้านการประกันชีวิตและประกันภัยอื่น ๆ แต่สมาคมดังกล่าวยังไม่ได้มีบทบาทในการดำเนินการจัดสอนวิชาชีพคณิตศาสตร์ประกันภัยโดยตรงเหมือนในอเมริกา แต่มีการให้วุฒิบัตรเป็น Fellow ของสมาคม โดยผู้ที่จะได้ต้องสำเร็จปริญญาตรีหรือสูงกว่าหลักสูตรคณิตศาสตร์ประกันภัย หรือสำเร็จหลักสูตรคณิตศาสตร์ประกันภัยจากสถาบันซึ่งสมาคมคณิตศาสตร์ประกันภัยรับรอง และหลังจากนั้นได้ปฏิบัติงานคณิตศาสตร์ประกันภัยมาแล้วเป็นเวลาไม่น้อยกว่า 5 ปี หรือไม่ก็เป็นสมาชิกระดับFellow ของสมาคมคณิตศาสตร์ประกันภัยที่นานาชาติรับรอง เช่น F.S.A. หรือ F.I.A. (Fellow จาก Institute of Actuaries ของสหราชอาณาจักร) และขณะนี้ยังดำรงสมาชิกภาพนั้นอยู่

ในอดีตที่ผ่านมา มีผู้สนใจและเห็นความสำคัญของการประกันชีวิตในประเทศไทยจำนวนน้อย สังเกตได้จากผู้สนใจทำประกันชีวิตเพียง 4% เท่านั้นจากประชากรทั้งหมด ซึ่งน้อยมากเมื่อเทียบกับอารยประเทศ เช่น อเมริกา ญี่ปุ่น ที่มีคนทำประกันชีวิตสูงมาก ประมาณ 200% ยิ่งคนไทยที่มีความรู้คณิตศาสตร์ประกันภัยยิ่งหายากมาก บริษัทประกันชีวิตส่วนใหญ่จึงต้องจ้างชาวต่างประเทศไทยมาเป็นที่ปรึกษา

ในช่วงเวลา 2 ปีที่ท่านมา การประกันชีวิตในประเทศไทยได้เจริญเติบโตขึ้นอย่างรวดเร็ว มีผู้สนใจและเห็นความสำคัญของการทำประกันชีวิตมากขึ้น จะเห็นได้จากในช่วง 3 เดือนแรกของปี 2532 มีอัตราการเติบโตถึง 28% เมื่อเทียบกับช่วงเดียวกันของปีที่แล้ว โดยพิจารณาจากเบี้ยประกันชีวิตรับโดยตรงของบริษัทประกันชีวิตทั้งหมด 12 บริษัท (รวมเบี้ยประกันภัยปีแรกและปีต่อไป) ประมาณ 3,129 ล้านบาท ซึ่งคาดการณ์ได้ว่าเมื่อรวมทั้งปีจะคิดเป็นเงินไม่ต่ำกว่าหมื่นล้านบาท เงินดังกล่าวนี้จะช่วยพัฒนาการลงทุนในประเทศและทำให้เศรษฐกิจส่วนรวมของประเทศเจริญเติบโตได้เป็นอย่างมาก

บทสรุป

จากข้อมูลที่กล่าวมาแล้วข้างต้นคงจะช่วยให้หลาย ๆ ท่านได้รู้จักนักคณิตศาสตร์ประกันภัย ตลอดจนบทบาทหน้าที่ ความรับผิดชอบที่มีต่อสังคมและต่อการดำเนินงานของธุรกิจประกันภัยให้ราบรื่น มั่นคง และเจริญก้าวหน้า อาจกล่าวได้ว่า ตราบใดที่ยังมีการค้าธุรกิจและการเสี่ยงภัยของครอบครัวซึ่งอาจจะเกิดจากการสูญเสียชีวิตของหัวหน้าครอบครัว ตราบนั้น นักคณิตศาสตร์ประกันภัยก็จะยังเป็นที่ต้องการอยู่ จึงไม่เป็นการผิดพลาดที่จะกล่าวว่า ปัญหาการเสี่ยงภัยของสังคมนั้นนับวันก็จะขยายวงกว้างออกไปทุกที ซึ่งจะก่อให้เกิดปัญหาที่จะต้องอาศัยนักคณิตศาสตร์ประกันภัยเพิ่มขึ้นเป็นเงาตามตัว แต่ในประเทศไทยขณะนี้ยังขาดแคลนผู้มีความรู้ ความสามารถด้านนี้อยู่ไม่น้อย ทั้งนี้อาจเป็นเพราะความไม่รู้ ไม่เข้าใจเกี่ยวกับบทบาท หน้าที่และความรับผิดชอบของนักคณิตศาสตร์ประกันภัยต่อธุรกิจประกันภัยและต่อสังคมก็เป็นได้

บทความนี้จึงเขียนขึ้นเพื่อมุ่งหวังให้บุคคลหลาย ๆ ฝ่ายที่เกี่ยวข้องทั้งนักคณิตศาสตร์ นักสถิติ นักธุรกิจ นักเศรษฐศาสตร์ ตลอดจนนักเรียน นักศึกษา และผู้สนใจจะเข้าสู่อาชีพนักคณิตศาสตร์ประกันภัย ซึ่งอาจไม่เคยมีความรู้มาก่อน หรือมีบ้างเล็กน้อยเกี่ยวกับอาชีพนักคณิตศาสตร์ประกันภัยได้มีความรู้ ความเข้าใจ และเห็นความสำคัญของนักคณิตศาสตร์ประกันภัย ช่วยกันส่งเสริมและเผยแพร่วิชาการด้านนี้ให้นักเรียน นักศึกษา นักวิชาการ และบุคคลทั่วไปที่สนใจได้รู้จัก และเข้าใจ เพื่อวันข้างหน้าในอนาคต ประเทศไทยจะได้มีนักคณิตศาสตร์ประกันภัยที่มีความสามารถ อันจะนำพาให้กิจการประกันภัยมีความเจริญก้าวหน้า เป็นหลักประกันความมั่นคงของสังคม ซึ่งจะส่งผลให้เศรษฐกิจของประเทศมีความมั่นคงและเจริญก้าวหน้า ทัดเทียมอารยประเทศในอนาคตอันใกล้นี้